Obsah

Porozumění matematickému procesu výpočtu objemu lichoběžníku prochází jádrem geometrie koncepční a praktické vědecké konstrukce. Níže uvedený text představuje postup krok za krokem, který má nejprve porozumět základním principům, které doprovázejí proměnné základní formulované rovnice, a poté je použít k řešení problémů s lichoběžníkovými obrazci.
Krok 1
Pochopte, že výstavba praktických projektů, jako jsou obytné nebo komerční budovy, zemní práce, jako jsou kalové lože a potrubí pro domácnost a další zařízení, zahrnuje nezbytné znalosti o objemu kapalných látek v uzavřených plochých číslech, které studentovi umožní pochopení potřeby výpočtu objemu. Přesné měření stávajících rozměrů vede k přesnému výpočtu objemu.
Praktickým způsobem je při definování lichoběžníku užitečné najít lichoběžníky jako průřezy hliněných stěn v geografické pánvi. Pokud jsou dvě strany čtyřstranné postavy rovnoběžné, ale nemají stejnou velikost a další dvě strany nejsou rovnoběžné, tato postava se nazývá lichoběžník.
Pokud tedy máte postavu, která je dlouhá 22,86 m, má čelní rozměr 17,37 m široký a 10,66 m vysoký a který má spodní část 21,94 m širokou a 3,65 m na výšku by bylo vypočítat objem takto:
Tvar lze považovat za obdélník 17,37 x 22,86 vpředu, spojený s 21,94 x 3,65 rovinami dole, ve vzdálenosti 22,86 m;
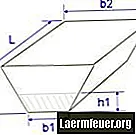
Vzorec pro výpočet objemu tímto způsobem, který lze nakreslit jako kufr s obdélníkovým horním a dolním dílem namísto zepředu a zezadu, lze vyjádřit jako V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3, kde proměnné lze popsat pomocí a1 = 17,37; bl = 10,66; a2 = 21,94; b2 = 3,65; h = 22,86: V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3 V = [17,3710,66 + 21,943,65 + (17,373,65 + 21,9410,66) / 2] * 22,86 / 3 V = [265,60 + (63,54 + 234,11) / 2] * 7,62 V = [265,60 + (297,66) / 2] 7,62 V = [414,44] 7,62 V = 3 158,03 m³
Krok 2
Po formátu se dynamický objem lichoběžníku liší od objemu statického modelu, protože statický lichoběžník je geometricky obrazec se dvěma rozměry. Vypočítávanou oblastí může být pouze lichoběžník navržený ve dvou rozměrech na papíře. Alternativní verze vzorce, která používá průměrnou šířku a délku, je tedy: V = [a1b1 + a2b2 + 4 ((a1 + a2) / 2 * (b1 + b2) / 2)] * h / 6 Obdélník má strany, které jsou průměrem stran horního a spodního obdélníku.)
Krok 3
Jako při dynamickém použití v kroku 2 lze objem lichoběžníkové konstrukce, jako je bazén nebo uzavřený válec, vypočítat jako litry na metr konkrétní výšky. To znamená, že objem plné nádoby dělený výškou má svůj vlastní důvod - použijte vzorec (s rozměry vm) k získání kubických metrů.
U libovolného kontejneru, který není válcový, se poměr bude lišit podle hloubky, pokud si to student přeje. A někdo by si mohl myslet, že to znamená, že nádoba bude částečně naplněna a že objem bude určen na různých úrovních. To znamená, že objem je funkcí výšky.
Krok 4
Jdeme trochu dále, protože šířka ve směru 'a' se lineárně mění z a1 na a2, a = a1 + (a2-a1) k = (1-k) a1 + ka2; jednotky kh stoupají zdola (kde k se pohybuje od 0 do 1); podobně b = bl + (b2-b1) k = (1-k) bl + kb2; objem tělesa s výškou kh, základnou a1 o b1 a nahoře a o b je V (k) = [a1b1 + ab + a1b / 2 + ab1 / 2] * kh / 3.
Pokud místo poměru k použijeme skutečnou hladinu kapaliny, můžeme dosadit k = L / ha dostaneme V (L) = [(3h ^ 2-3Lh + L ^ 2) a1b1 + L ^ 2a2b2 + (3Lh-2L ^ 2) (a1b2 + a2b1) / 2] * L / (3h ^ 2). To nám dává objem jako funkci hloubky.
Krok 5
Správný výpočet objemu lichoběžníku zahrnuje schopnost interpretovat, zda je lichoběžníkový obraz dvojrozměrný nebo trojrozměrný. Dynamická praxe technického lichoběžníkového interpretačního aspektu se točí kolem toho, zda je lichoběžníkový obraz něco, co je jednoduše navrženo nebo zkonstruováno, zda obsahuje svazek nebo je to pouze skica na papíře.