Obsah
- Určete čas ve vzduchu.
- Krok 1
- Krok 2
- Krok 3
- Krok 4
- Určete maximální výšku
- Krok 1
- Krok 2
- Krok 3
- Určete vodorovnou ujetou vzdálenost.
- Krok 1
- Krok 2
- Krok 3
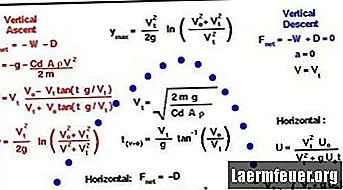
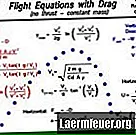
Zde je metoda výpočtu trajektorie střely, konkrétně času ve vzduchu, dosahu a nejvyššího bodu její trajektorie. V tomto příkladu byly učiněny některé předpoklady pro zjednodušení výpočtu: zanedbatelný odpor vzduchu, bezvětří a nedostatečná palebná vzdálenost, aby se mohla projevit rotace Země.
Určete čas ve vzduchu.
Krok 1
Nejprve je třeba určit tvar luku. Pokud je úhel zpočátku dolů, je již známo, že nejvyšším bodem je palebná poloha. Dokonce i úhel vzhůru může mít cíl jako nejvyšší bod, ať už je tento úhel mělký nebo dostatečné výšky (h). To lze určit v kroku čtyři, kdy se určuje vysílací čas.
Krok 2
Pokud je úhel „?“ rychlost střelby je ta mezi počáteční dráhou střely a vodorovnou, takže počáteční svislá rychlost je V (i) = V.sen?.
Krok 3
Vysílací čas se zjistí pomocí rovnice polohy h = V.sen?. T - (0,5) g.t ^ 2, kde g = 9,8 metrů / s ^ 2. Všechny proměnné jsou známy, s výjimkou času ve vzduchu, t, takže to lze vyřešit pomocí kvadratické funkce: ax ^ 2 + bx + c = 0, tedy x = [-b ± √ (b ^ 2-4ac )] / 2a
Krok 4
Pokud je povoleno více než jedno řešení pro t, protože h> 0, pak první výsledek odpovídá, když height = h na cestě výstupu, a druhý, když height = h na cestě sestupu. Pokud h <0, pak bylo povoleno jediné skutečné řešení pro t a druhé je záporné.
Určete maximální výšku
Krok 1
Pokud? <0, je již známo, že maximální výška je počáteční výška, h = 0.
Krok 2
Pokud bylo více než jeden čas, t, ve kterém kulka zasahuje h, pak nejmenší t odpovídá dráze letu, kde h je nejvyšší bod. Nejvyšší t odpovídá střele, která dosáhla vyšší výšky před návratem do h, k vyřešení této výšky použijte vzorec V (t) = V (0) - 9,8 t k nalezení hodnoty t, když je vertikální rychlost nula. Jinými slovy, za jakou dobu, t, V.sen? = 9,8 t.?
Krok 3
Řešení t a připojení výškového vzorce máme maximální výšku: hm = V.sen? - 4,9 t ^ 2. Stejný přístup se používá pro řešení maximální výšky, pokud bylo povoleno pouze jedno řešení pro t.
Určete vodorovnou ujetou vzdálenost.
Krok 1
Chcete-li určit vodorovnou vzdálenost uraženou v době, kdy střela dosáhne výšky h, nejprve vypočítejte počáteční vodorovnou rychlost střely: v (i) = V.cos (?).
Krok 2
Nahraďte čas, t, když kulka dosáhne konečné výšky, A, v poloze vzorce pomocí horizontální rychlosti: A = V.cosΘ.t. Za předpokladu, že na pravé straně není žádný odpor vzduchu a žádný výraz zrychlení.
Krok 3
Pokud tam byla více než jedna doba t, když byla výška v h, pak budou platné dvě polohy „A“, přičemž nejvyšší dosažený bod bude hm pro menší ze dvou „A“. Nyní jsou známy vodorovné a svislé koncové polohy a nejvyšší dosažený bod, což určuje trajektorii střely.